Skip to main content

笔记

基本运算​

ln⁡(x)\ln(x)​

ln⁡(ab)=ln⁡a+ln⁡b,ln⁡(ab)=ln⁡a−ln⁡b,ln⁡(ab)=bln⁡a\ln(ab) = \ln a + \ln b , \ln\left(\frac{a}{b}\right) = \ln a - \ln b , \ln(a^b) = b \ln a 常用公式:ln⁡x=12ln⁡xln⁡1x=−ln⁡xln⁡(1+1x)=ln⁡x+1x=ln⁡(x+1)−ln⁡x\begin{aligned} \text{常用公式}:\ln\sqrt{x}&=\frac{1}{2}\ln x \\ \ln\frac{1}{x}&=-\ln x \\ \ln\biggl(1+\frac{1}{x}\biggr)&=\ln\frac{x+1}{x}=\ln(x+1)-\ln x \end{aligned}

xnx^n​

aα∙aβ=aα+β,aαaβ=aα−β,(aα)β=aαβ,(ab)α=aαbα,(ab)α=aαbα\begin{aligned} a^{\alpha}\bullet a^{\beta}=a^{\alpha+\beta} , \frac{a^{\alpha}}{a^{\beta}}=a^{\alpha-\beta} , (a^{\alpha})^{\beta}=a^{\alpha\beta} , (ab)^{\alpha}=a^{\alpha}b^{\alpha} , \left(\frac{a}{b}\right)^{\alpha}=\frac{a^{\alpha}}{b^{\alpha}} \end{aligned} 常用公式:x=eln⁡x(x>0)uν=eln⁡uν=eνln⁡u(u>0)\begin{aligned} \text{常用公式}:x&=\mathrm{e}^{\ln x}(x>0)\\ u^{\nu}&=\mathrm{e}^{\ln u^{\nu}}=\mathrm{e}^{\nu\ln u}(u>0) \end{aligned}

重要极限公式​

lim⁡x→0+xαln⁡\lim_{\mathrm{x}\to0^+}\mathrm{x}^\alpha\lnx=0 其中a>0a>0

lim⁡x→0+\operatorname* { lim} _{\mathbf{x} \to 0^{+ }} xα(ln⁡\mathbf{x} ^{\alpha }( \lnx)k=0) ^\mathrm{k} = 0 其中α>0\alpha > 0, k>0\mathbf{k} > 0

lim⁡x→+∞\lim _{\mathrm{x} \to + \infty } xαe−δxx^{\alpha }e^{- \delta \mathrm{x} }= 0 其中α>0\alpha > 0, δ>0\delta > 0

lim⁡x→0sin⁡xx=1\lim _{\mathrm{x\to 0}}\frac {\sin \mathrm{x} }{\mathrm{x} }= 1 ⟹lim⁡ϕ(x)→0sin⁡ϕ(x)ϕ(x)=1\Longrightarrow \lim _{\mathrm{\phi ( x) \to 0}}\frac {\sin \mathrm{\phi ( x) }}{\mathrm{\phi ( x) }}= 1 其中ϕ(\phi(x)≠0)\neq0

lim⁡x→0(1+\lim_{\mathrm{x\to0}}(1+x)1x=)^\frac1x=e ⟹lim⁡ϕ(x)→0(1+ϕ(\Longrightarrow \lim _\mathrm{\phi ( x) \to 0}( 1+ \phi (x))1ϕ(x)=))^\frac1{\phi(x)}=e 其中ϕ(\phi(x)≠0)\neq0

lim⁡n→∞nn=1\lim_{\text{n}\to\infty}\sqrt[\text{n}]{\text{n}}=1

lim⁡n→∞an=1\lim _{\mathrm{n} \to \infty }\sqrt [ n] {\mathrm{a} }= 1 (常数a>0)

x→0.ex−1∼x {x\rightarrow0.e^{x}-1\sim x} f(x)→0.ef(x)−1∼f(x){f(x)\rightarrow0.e^{f(x)}-1\sim f(x)} lim⁡x→0x−sin⁡x=16x3\lim_{x\to0}x-\sin x=\frac{1}{6}{x^{3}}

常用等价无穷小(求极限)​

x→0\to0时，

sin⁡x∼tan⁡x∼arcsin⁡x∼arctan⁡x∼(ex−1)∼ln⁡(1+x)∼x \sin\mathrm{x}\sim\tan\mathrm{x}\sim\arcsin\mathrm{x}\sim\arctan\mathrm{x}\sim(\mathrm{e}^\mathrm{x}-1)\sim\ln(1+\mathrm{x})\sim\mathrm{x}\:  1−cos⁡x∼12x2 \:1-\cos\mathrm{x}\sim\frac{1}{2}\mathrm{x}^2\: (1+x)a−1∼ax (1+x)^a-1\sim ax~  ax−1∼xln⁡a (a>0,a≠1)~a^x-1\sim x\ln a~(a>0,a\neq1)

alt text

(x)′(x)\prime基本初等函数的导数公式​

(xa)′=axa−1(a为常数)(ax)′=axln⁡a(ex)′=ex(log⁡ax)′=1xln⁡a(a>0,a≠1)(ln⁡x)′=1x(sin⁡x)′=cos⁡x(cos⁡x)′=−sin⁡x(arcsin⁡x)′=11−x2(arccos⁡x)′=−11−x2(tan⁡x)′=sec⁡2x(cot⁡x)′=−csc⁡2x(arctan⁡x)′=11+x2(arccot⁡x)′=−11+x2(sec⁡x)′=sec⁡x⋅tan⁡x(csc⁡x)′=−csc⁡x⋅cot⁡x[ln⁡(x+x2+1)]′=1x2+1[ln⁡(x+x2−1)]′=1x2−1\begin{aligned} (x^a) ^\prime &=ax^{a- 1} (a为常数) \\ ( a^x) ^\prime &= a^x\ln a \\ (\mathrm{e}^{\mathrm{x}})^{\prime} &=\mathrm{e}^{\mathrm{x}} \\ (\log_{\mathrm{a}}x) ^\prime &= \frac 1{\mathrm{x} \ln \mathrm{a} } (a>0,a\neq1) \\ (\ln x )^\prime &=\frac1x \\ (\sin x )^\prime &=\cos x \\ (\cos x )^\prime &=-\sin x \\ \left(\arcsin\text{x}\right)^{\prime} &=\frac1{\sqrt{1-\mathrm{x}^2}} \\ (\arccos x )^\prime &=-\frac1{\sqrt{1-\mathrm{x}^2}} \\ (\tan x )^\prime &=\sec^2 x \\ \left(\cot\text{x}\right)^{\prime} &=-\csc^2 x \\ (\arctan x )^\prime &=\frac1{1+\mathrm{x}^2} \\ (\operatorname{arccot} x )^\prime &=-\frac1{1+\mathrm{x}^2} \\ \left ( \sec \text{x}\right ) ^{\prime } &= \sec x \cdot \tan x \\ \left(\csc x\right)^{\prime} &=-\csc x\cdot\cot x \\ [\ln(\mathrm x+\sqrt{\mathrm x^2+1})]' &=\dfrac{1}{\sqrt{\mathrm x^2+1}} \\ [\ln(\mathrm x+\sqrt{\mathrm x^2-1})]' &=\dfrac{1}{\sqrt{\mathrm x^2-1}} \end{aligned}

高阶导数的运算​

[u±v](n)=u(n)±v(n)\mathrm{[u\pm v]^{(n)}=u^{(n)}\pm v^{(n)}} (uv)(n)=u(n)v+Cn1u(n−1)v′+Cn2u(n−2)v′′+...+Cnku(n−k)v(k)+...+Cnn−1u′v(n−1)+uv(n)=∑k=0nCnku(n−k)v(k)\begin{aligned}\left(\mathrm{uv}\right)^{\left(\mathrm{n}\right)}&=\mathrm{u^{(n)}v+C_n^1u^{(n-1)}v^{\prime}+C_n^2u^{(n-2)}v^{\prime\prime}+...+C_n^ku^{(n-k)}v^{(k)}+...+C_n^{n-1}u^{\prime}v^{(n-1)}+uv^{(n)}}\\&=\sum_{\mathrm{k=0}}^\mathrm{n}\mathrm{C_n^ku^{(n-k)}v^{(k)}}\end{aligned}

∫\int 基本积分公式​

以下公式中,α\alpha与aa均为常数,除声明者外,a>0a>0

∫xadx=1α+1xα+1+C(α≠−1)∫1xdx=ln⁡∣x∣+C∫axdx=axln⁡a+C (a>0,a≠1)∫exdx=ex+C∫sin⁡xdx=−cos⁡x+C∫cos⁡xdx=sin⁡x+C∫tan⁡xdx=−ln⁡cos⁡∣x∣+C∫cot⁡xdx=ln⁡∣sin⁡x∣+C∫sec⁡xdx=ln⁡∣sec⁡x+tan⁡x∣+C∫csc⁡xdx=ln⁡∣csc⁡x−cot⁡x∣+C∫sec⁡2xdx=tan⁡x+C∫csc⁡2xdx=−cot⁡x+C∫1a2+x2dx=1aarctan⁡xa+C∫1a2−x2dx=12aln⁡∣a+xa−x∣+C∫1a2−x2dx=arcsin⁡xa+C∫1x2±a2 dx=ln⁡∣x+x2±a2∣+C\begin{aligned} \int\mathrm x^a\mathrm d\mathrm x&=\frac{1}{\alpha+1}\mathrm x^{\alpha+1}+\mathrm C\quad(\alpha\neq-1) \\ \int\frac{1}{\mathrm{x}}dx&=\ln|x|+C \\ \int a^{x}dx&=\frac {a^{x}}{\ln a}+ C\:( a> 0, a\neq1) \\ \int e^xdx&= e^x+ C \\ \int\sin\mathrm{xdx}&=-\cos\mathrm{x}+\mathrm{C} \\ \int\cos\mathrm{xdx}&=\sin\mathrm{x}+\mathrm{C} \\ \int\tan xdx&=-\ln\cos |x|+C \\ \int\cot\mathrm{xdx}&=\ln|\sin\mathrm{x}|+\mathrm{C} \\ \int\sec\mathrm{xdx}&=\ln|\sec\mathrm{x}+\tan\mathrm{x}|+\mathrm{C} \\ \int\csc\mathrm{xdx}&=\ln|\csc\mathrm{x}-\cot\mathrm{x}|+\mathrm{C} \\ \int\sec^{2}xdx&=\tan x+C \\ \int\csc^{2}xdx&=-\cot x+C \\ \int\frac{1}{\mathrm{a}^{2}+\mathrm{x}^{2}}dx&=\frac1{\mathrm{a}}\arctan\frac{\mathrm{x}}{\mathrm{a}}+C \\ \int\frac{1}{\mathrm{a}^{2}-\mathrm{x}^{2}}dx&=\frac1{2\mathrm{a}}\ln|\frac{\mathrm{a}+\mathrm{x}}{\mathrm{a}-\mathrm{x}}|+C \\ \int\frac{1}{\sqrt{\mathrm{a}^{2}-\mathrm{x}^{2}}}dx&=\arcsin\frac{\mathrm{x}}{\mathrm{a}}+C \\ \int\frac1{\sqrt{\mathrm{x}^2\pm\mathrm{a}^2}}\:\mathrm{dx}&=\ln|\mathrm{x}+\sqrt{\mathrm{x}^2\pm\mathrm{a}^2}|+\mathrm{C} \end{aligned}

∫\int 重要积分公式​

∫−∞+∞ e−x2dx=2∫0+∞ e−x2dx=π\int_{-\infty}^{+\infty}\mathrm{~e^{-x^2}dx}=2\int_0^{+\infty}\mathrm{~e^{-x^2}dx}=\sqrt{\pi}

∫0+∞xne−xdx=n!\int_0^{+\infty}\mathrm{x^ne^{-x}dx=n!}

∫−aaf(x)dx=∫0a[f(x)+f(−x)]dx\mathrm{\int_{-a}^af(x)dx=\int_0^a[f(x)+f(-x)]dx}

∫0πxf(sin⁡x)dx=π2∫0πf(sin⁡x)dx=π∫0π2f(sin⁡x)dx\int_0^\pi\mathrm{xf(\sin x)dx}=\frac\pi2\int_0^\pi\mathrm{f(\sin x)dx}=\pi\int_0^{\frac\pi2}\mathrm{f(\sin x)dx}

∫abf(x)dx=(b−a)∫01f[a+(b−a)x]dx\int_\mathrm{a}^\mathrm{b}\mathrm{f(x)dx}=(\mathrm{b-a})\int_0^1\mathrm{f[a+(b-a)x]dx}

泰勒公式​

  • 泰勒公式

    f(x)=f(a)0! + f′(a)1! (x−a) + f′′(a)2! (x−a)2 + ... + f(n)(a)n! (x−a)n + Rn(x)=lim⁡n→∞∑i=0nf(n)(a)n!(x−a)n\begin{aligned}\mathrm{f(x)}&=\frac{\mathrm{f(a)}}{0!}\:+\:\frac{\mathrm{f'(a)}}{1!}\:(\mathrm{x}-\mathrm{a})\:+\:\frac{\mathrm{f''(a)}}{2!}\:(\mathrm{x}-\mathrm{a})^{2}\:+\:...\:+\:\frac{\mathrm{f^{(n)}(a)}}{\mathrm{n!}}\:(\mathrm{x}-\mathrm{a})^{\mathrm{n}}\:+\:\mathrm{R_{n}(x)}\\&=\lim_{\mathrm{n\to\infty}}\sum_{\mathrm{i=0}}^{\mathrm{n}}\frac{\mathrm{f^{(n)}(a)}}{\mathrm{n!}}\left(\mathrm{x-a}\right)^{\mathrm{n}}\end{aligned}

  • 拉格朗日余项的泰勒公式

    f(x)=f(a)0!+f′(a)1!(x−a)+f′′(a)2!(x−a)2+...+f(n)(a)n!(x−a)n+f(n+1)(ξ)(n+1)!(x−a)n+1\mathrm{f(x)=\frac{f(a)}{0!}+\frac{f'(a)}{1!}\left(x-a\right)+\frac{f''(a)}{2!}\left(x-a\right)^2+...+\frac{f^{(n)}(a)}{n!}\left(x-a\right)^n+\frac{f^{(n+1)}(\xi)}{(n+1)!}\left(x-a\right)^{n+1}}

    其中ξ\xi介于x，a之间

  • 佩亚诺余项的泰勒公式

    f(x)=f(a)0!+f′(a)1!(x−a)+f′′(a)2!(x−a)2+...+f(n)(a)n!(x−a)n+o((x−a)n)\mathrm{f(x)=\frac{f(a)}{0!}+\frac{f'(a)}{1!}(x-a)+\frac{f''(a)}{2!}(x-a)^2+...+\frac{f^{(n)}(a)}{n!}(x-a)^n+o((x-a)^n)}

常用的泰勒展开式​

sin⁡x=x−x33!+o(x3)cos⁡x=1−x22!+x44!+o(x4)arcsin⁡x=x+x33!+o(x2)tan⁡x=x+x33+o(x2)tan⁡x=x+x33+o(x2)arctan⁡x=x−x33+x55+o(x5)(1+x)a=1+ax+a(a−1)2!x2+o(x2)11−x=1+x+x2+x3+o(x3)11+x=1−x+x2−x3+o(x3)ln⁡(1+x)=x−x22+x33−x44+o(x4)11+x2=1−x2+x4−x6+o(x6)ex=1+x+x22!+x33!+o(x3)\begin{aligned}&\sin\mathrm{x}=\mathrm{x}-\frac{\mathrm{x}^3}{3!}+\mathrm{o}(\mathrm{x}^3)\\&\cos\mathrm{x}=1-\frac{\mathrm{x}^2}{2!}+\frac{\mathrm{x}^4}{4!}+o(\mathrm{x}^4)\\&\arcsin\mathrm{x}=\mathrm{x}+\frac{\mathrm{x}^3}{3!}+o(\mathrm{x}^2)\\&\tan\mathrm{x}=\mathrm{x}+\frac{\mathrm{x}^3}3+o(\mathrm{x}^2)\\&\tan\mathrm{x}=\mathrm{x}+\frac{\mathrm{x}^3}3+o(\mathrm{x}^2)\\&\arctan\mathrm{x}=\mathrm{x}-\frac{\mathrm{x}^3}3+\frac{\mathrm{x}^5}5+o(\mathrm{x}^5)\\&(1+\mathrm{x})^a=1+a\mathrm{x}+\frac{a(a-1)}{2!}\mathrm{x}^2+o(\mathrm{x}^2)\\&\frac1{1-\mathrm{x}}=1+\mathrm{x}+\mathrm{x}^2+\mathrm{x}^3+o(\mathrm{x}^3)\\&\frac1{1+\mathrm{x}}=1-\mathrm{x}+\mathrm{x}^2-\mathrm{x}^3+o(\mathrm{x}^3)\\&\ln(1+\mathrm{x})=\mathrm{x}-\frac{\mathrm{x}^2}2+\frac{\mathrm{x}^3}3-\frac{\mathrm{x}^4}4+o(\mathrm{x}^4)\\&\frac1{1+\mathrm{x}^2}=1-\mathrm{x}^2+\mathrm{x}^4-\mathrm{x}^6+o(\mathrm{x}^6)\\&\mathrm{e}^{\mathrm{x}}=1+\mathrm{x}+\frac{\mathrm{x}^2}{2!}+\frac{\mathrm{x}^3}{3!}+o(\mathrm{x}^3)\end{aligned}

口诀：指对连，三角断，三角对数隔一换，三角指数有感叹，反三角它同又乱

指对连：指数函数、对数函数，都是12345连续的

三角断：三角函数的展开式是135，246这样不连续的三角对数隔一换：三角函数和对数函数的符号隔一个换一次

三角指数有感叹：三角函数和指数函数中分母有阶层 (感叹号)

反三角它同又乱：反三角函数的和三角函数第一项相同，第二项为相反数

结论​

1◯x→0 时,ln⁡(x+x2+1)∼x.2◯[ln⁡(x+x2+1)]′=1x2+1,于是∫1x2+1dx=ln⁡(x+x2+1)+C.3◯由于y=ln⁡(x+x2+1)是奇函数,于是∫−11[ln⁡(x+x2+1)+x2]dx=∫−11x2dx=23\begin{aligned} &\textcircled{1}x\to0\text{ 时,}\ln\left(x+\sqrt{x^{2}+1}\right)\sim x . \\ &\textcircled{2}\left[\ln\left(x+\sqrt{x^{2}+1}\right)\right]^{\prime}=\frac{1}{\sqrt{x^{2}+1}} , \text{于是}\int\frac{1}{\sqrt{x^{2}+1}}\mathrm{d}x=\ln\left(x+\sqrt{x^{2}+1}\right)+C . \\ &\textcircled{3}\text{由于}y=\ln\left(x+\sqrt{x^2+1}\right)\text{是奇函数,于是}\int_{-1}^{1}\left[\ln\left(x+\sqrt{x^2+1}\right)+x^2\right]\mathrm{d}x=\int_{-1}^{1}x^2\mathrm{d}x=\frac{2}{3} \end{aligned}

反双曲正弦函数&双曲正弦函数​

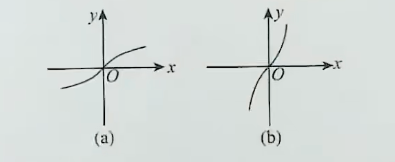
函数y=ln⁡(x+x2+1)y=\ln\left(x+\sqrt{x^2+1}\right)叫作反双曲正弦函数，其图像如图 I-3(a)所示 .函数 y=ex−e−x2y=\frac{\mathrm{e}^x-\mathrm{e}^{-x}}2 叫作双曲正弦函数，其图像如图 1-3(b)所示 .考生应记住这两个函数的图像.

双曲余弦函数​

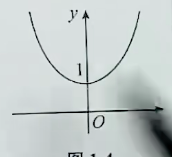
(2)y=ex+e−x2(2)y=\frac{\mathrm{e}^x+\mathrm{e}^{-x}}{2}叫作双曲余弦函数，其图像如图 1-4所示，它是偶函数，是一种特殊的悬链线，约翰·伯努利解决了这个问题那不是抛物线y=x2y=x^2,而是悬链线y=α2(exα+exα)y=\frac\alpha2\left(\mathrm{e}^{\frac x\alpha}+\mathrm{e}^{\frac x\alpha}\right),取a=1a=1,便是此例.

求他们的反函数​

y=ln⁡(x+x2+1)−y=−ln⁡(x+x2+1)−y=ln⁡(x−x2+1)(x+x2+1)(x−x2+1)−y=ln⁡(x2+1−x)1ey=x+x2+11◯e−y=x2+1−x2◯1◯−2◯⇒ey−e−y=2x⇒x=ey−e−y2y=\ln(x+\sqrt{x^{2}+1})\\-y=-\ln(x+\sqrt{x^{2}+1})\\-y=\ln\frac{(x-\sqrt{x^{2}+1})}{(x+\sqrt{x^{2}+1})(x-\sqrt{x^{2}+1})}\\-y=\ln\frac{(\sqrt{x^{2}+1}-x)}{1}\\e^{y}=x+\sqrt{x^{2}+1}\textcircled{1}\\e^{-y}=\sqrt{x^{2}+1}-x\textcircled{2}\\\textcircled{1}-\textcircled{2}\Rightarrow e^{y}-e^{-y}=2x\Rightarrow x=\frac{e^{y}-e^{-y}}{2}

隐函数​

设方程F(x,y)=0F(x,y)=0 ,若当xx 取某区间内的任一值时，总有满足该方程的唯一的值yy存在，则称方程F(x,y)=0F(x,y)=0在上述区间内确定了一个隐函数y=y(x)y= y( x) . 如x+y3−1=0x+y^3-1=0 就表示一个隐函数，且可显化为y=1−x3;y=\sqrt[3]{1-x};再如sin⁡(xy)=ln⁡x+ey+1\sin(xy)=\ln\frac{x+e}{y}+1 也表示一个隐函数，但不易显化. 一般来说，由F(x,y)=0F(x,y)=0 所确定的隐函数求 y(x0)y(x_0),若代人x0x_0易求出y(x0)y(x_0),则直接求之；若不易求出y(x0)y(x_0),则用观察法.如：

1◯设函数y=y(x)由方程ln⁡y−xy+x=0确定,当x=2时,y(2)=12◯设函数y=y(x)由方程ln⁡y+ey−1=x2确定,当x=2时,y(2)=1\textcircled{1}\text{设函数}y=y(x)\text{由方程}\ln y-\frac{x}{y}+x=0\text{确定,当}x=2\text{时,}y(2)=1\\\textcircled{2}\text{设函数}y=y(x)\text{由方程}\ln y+\mathrm{e}^{y-1}=\frac{x}{2}\text{确定,当}x=2\text{时,}y(2)=1

思路​

碰到 ln 想到负号以变成倒数来求

复合函数f(x)g(x)f(x)g(x)可以当作运算符

出现ln⁡\ln时可以用1=ln⁡e1=\ln e来凑,也可能 sin⁡2α+cos⁡2α=1\sin^2\alpha+\cos^2\alpha=1

给出exe^x求axa^x要变换成exln⁡ae^{x\ln a} (ex=∑n=0∞xnn!\mathrm{e}^{x}=\sum_{n=0}^{\infty}\frac{x^{n}}{n!})

没思路可以尝试逆运算

u(x)v(x)=⁡100%ev(x)ln⁡u(x)u(x)^{v(x)}\overset{100\%}{\operatorname*{=}}e^{v(x)\ln u(x)}

注意​

∞是两个点，要小心，因为函数唯一性\infin \text{是两个点，要小心，因为函数唯一性}

平方后开根号是绝对值

u2=∣u∣\sqrt{u^{2}}=|u|